Arch Analysis
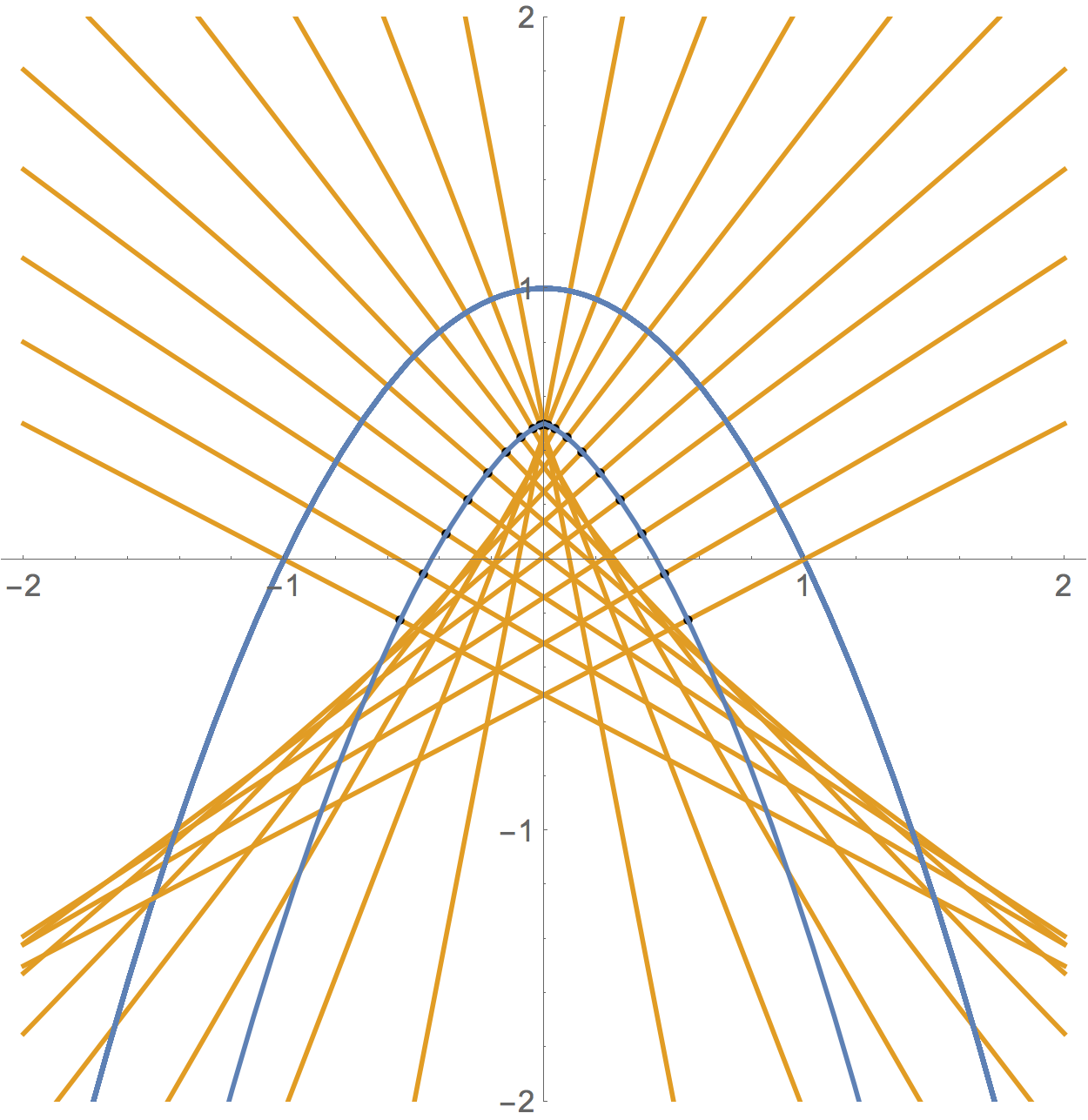
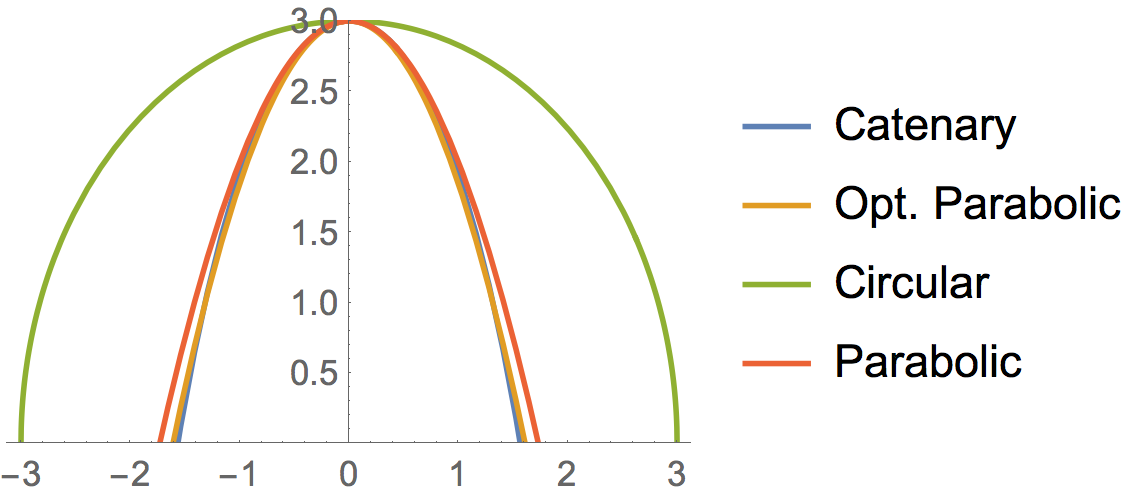
This project grew out of my fascination withs arches. The catenary arch is known to be the optimal self-supporting arch, and the third image shown below compares it with a few other arches. The parabolic arch is defined by the equation y = x^2, however constructing a parabolic arch with thickness (as opposed to just the curve) is not entirely simple. In this context parallel means a constant distance in a direction that is perpendiular to the parabola (the orange lines show the perpendicular direction and the black dots indicate the new curve being formed). Using this definition, it's possible to derive the analytic expression for the parallel curve and it turns out to not be a parabola (the curve doesn't have a name).
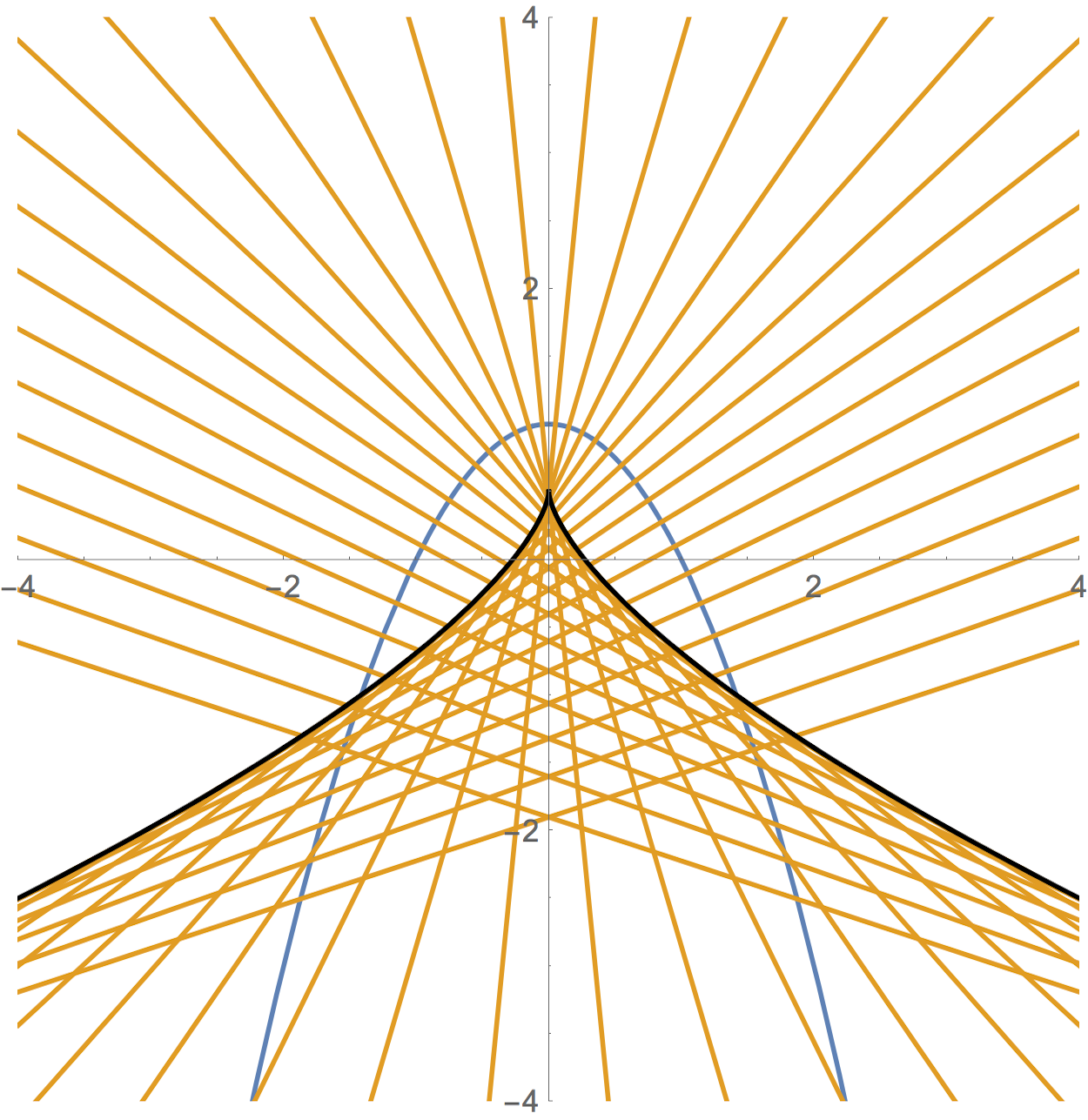
The shrewd observer will notice that there seems to be another interesting curve formed by the norm rays, it's outline in black in the second image. This curve as it turns out is an example of a caustic. The term exists in mathematics (basically defined as the envelope of these normal rays), and also in optics, here. Actually, it turns out embedding these caustic curves into a material is an active area of research, see for example this paper.