Bezier Patch Pathfinding
This project gives one approach for solving the pathfinding problem (geodesic equations) via the
shooting-method for nonlinear boundary value problems.
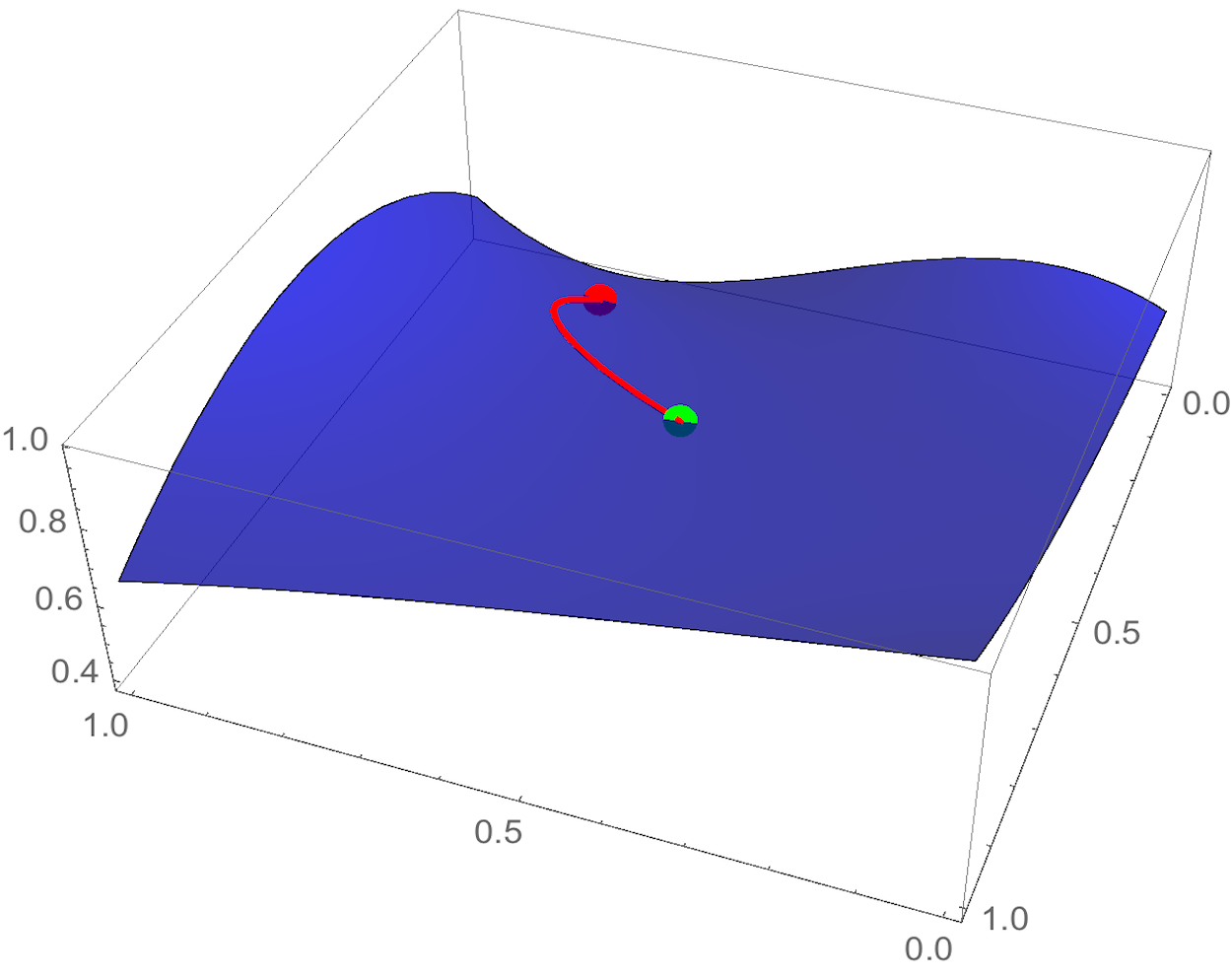
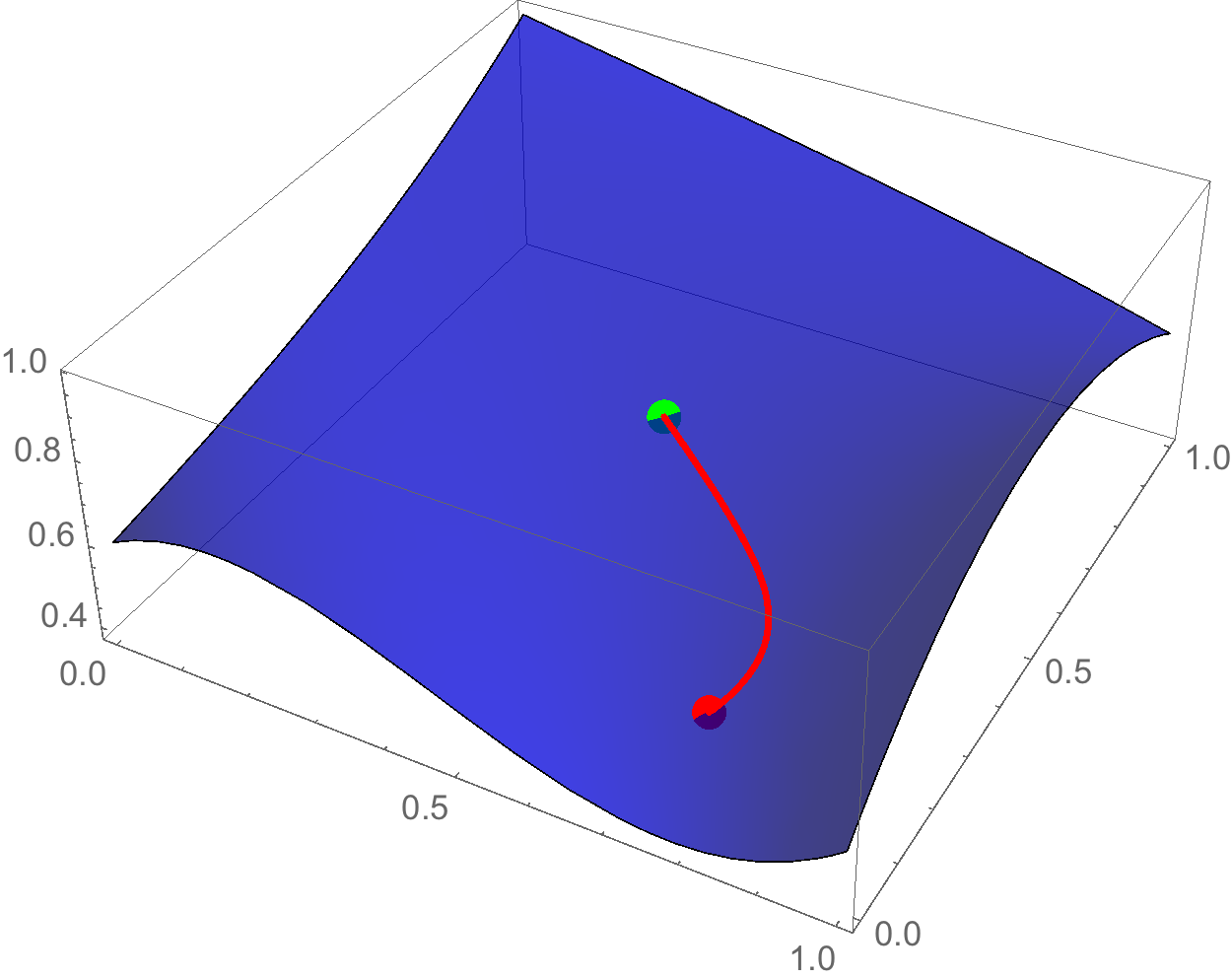
Mathematically, a boundary value problem is when you have some equations and you want to specify the solution at several different points. For example, on my Bezier Patch, I want a path between two points such that the length of the path is as small as it can be. For contrast, consider the initial value problem: given an initial position and velocity (in particular the direction of the velocity), what path will I follow? The first problem is harder because there's no initial direction specified.
So the strategy here is guess some initial velocity, and if it takes me exactly to the point I want to end up at, that's great and I'm done. But if I don't end up at the point, I'll have to guess a new initial velocity. This is the shooting-method with the condition that the "guessing" is done by root-finding methods (like Newton's method).
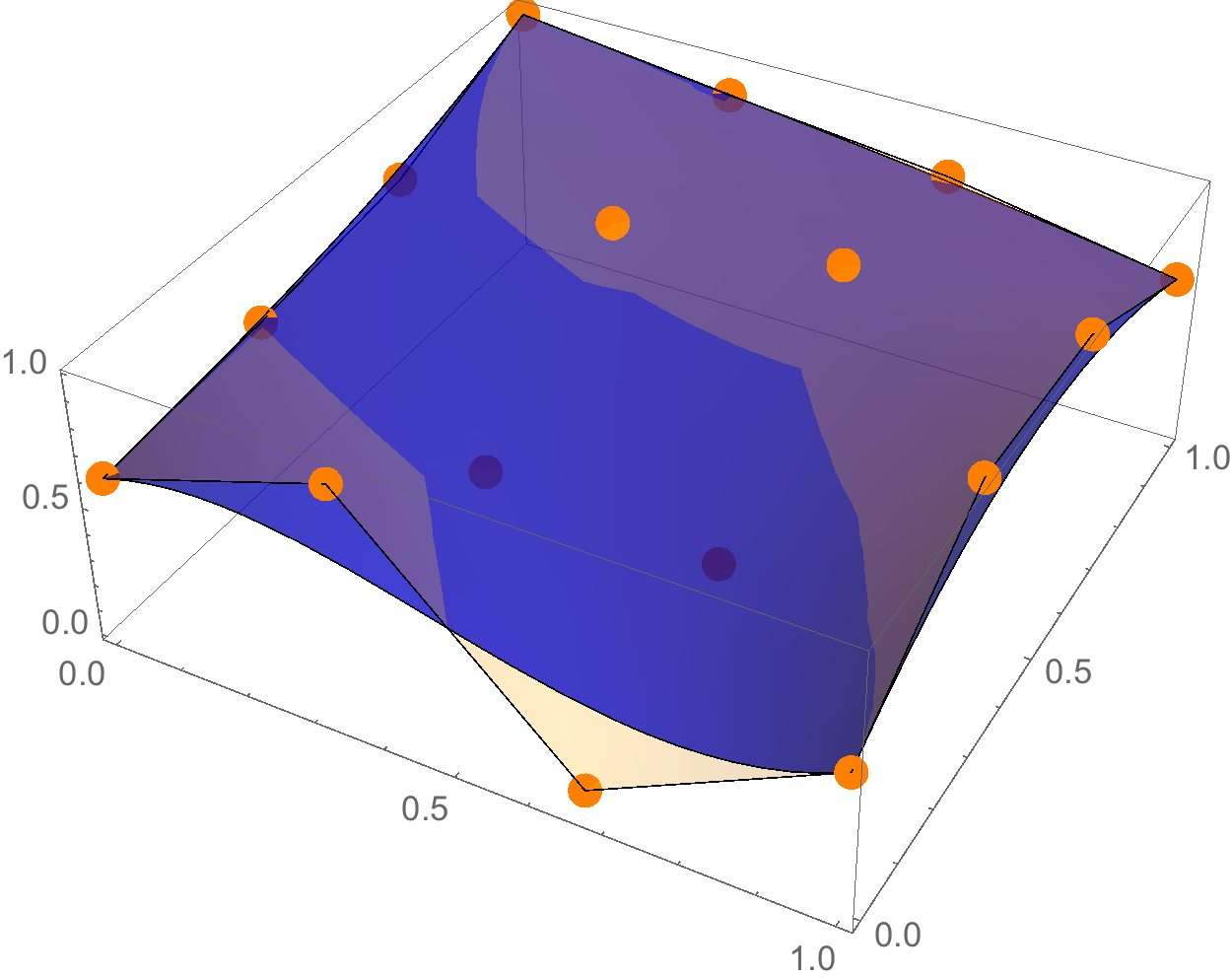
The third picture shows the 16 control points of the Bezier Patch, and a triangulation of those points, as opposed to the smooth Bezier patch in blue.